Using a GDO
===========

This page describes how to use a GDO or Grid Dip Oscillator. Most of the description and the diagrams were taken from an old User Manual published by Barker and Williamson of Pensylvania in, I would guess, about 1952. If they or anyone holding the copyright wishes me to remove this page then I will do so. If anyone notices any errors, spelling or otherwise, please let me know, my e-mail address is on my home page

LC Circuits
===========
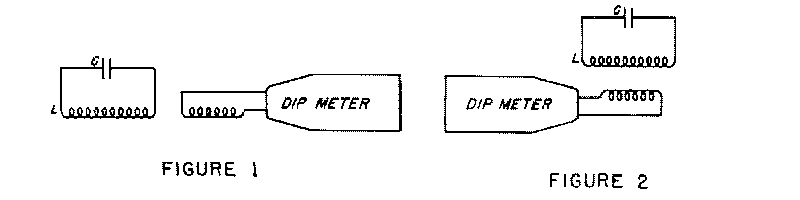
The main use of the instrument when used as a dip meter is to indicate the resonant frequency of a tuned circuit. This is done by placing the coil of the instrument in close inductive proximity to the coil of the circuit being measured, and rotating the tuning knob until a sharp dip is noted in the meter. See Fig1 and Fig2.

The sensitivity control is used to keep the meter reading approximately in mid scale. When the position of the meter dip is ascertained, the coil distance is increased until the dip is barely disernable. The resonant frequency of the circuit being measured can then be approximated from the appropriate dial scale, and accurately measured with a Digital Frequency Meter or by locating the signal on a calibrated reciever.
The above procedure is used in finding the resonant frequency of:

1. Traps and chokes
2. Tank circuits
3. I.F. circuits
4. R.F. circuits
5. Filters (high, low and band-pass) etc.

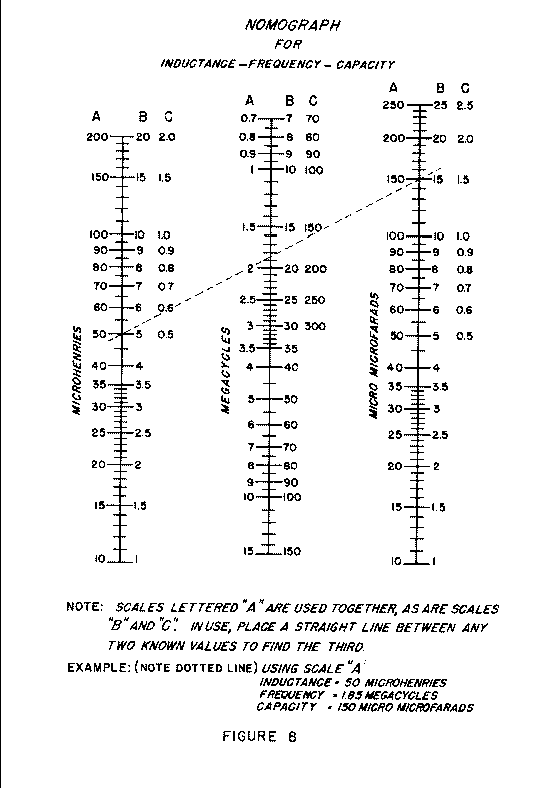
After the resonant frequency of a tuned circuit has been determined, the inductance or capacitance may be found if one or the other is known. The nomograph (see fig8) relating inductance, capacitance and frequency has been prepared to facilitate this procedure or it can be calculated using the formulae:

L = 25400 / (f*f)*C or C = 25400 / (f*f)*L or f = 1 / 6.284*(square root of (L*C))

where f is Frequency in Mhz, C is in Picofarads, L is in microHenries.

Known values of capacity can be purchased for use as standards, or established by the use of known values of inductance. Standard inductances can be fabricated by using standard capacitors.
Note that the approximate "Q" or quality of resonant circuits may be compared by observing the sharpness of the meter dip as the tuning is rotated through resonance. A sharp dip indicates a circuit of higher "Q" than one with a broad dip.
When used on transistor equipment it may be useful to either isolate the circuit under test or to use the instrument as an Adsorbtion Wave Meter, see later, and have the circuit under test operating, this is due to the low impeadances often seen in semiconductor circuits.

Antennas and Transmission Lines
===============================
Antennas and transmission lines differ from lumped LC circuits in that the inductance and capacity is distributed. It is important to remember that more than one resonant frequency is present which must be taken into concideration. It is advantageous to determine in advance the approximate frequencies of interest and sketch the antenna and transmission line set-up in terms of current distribution.
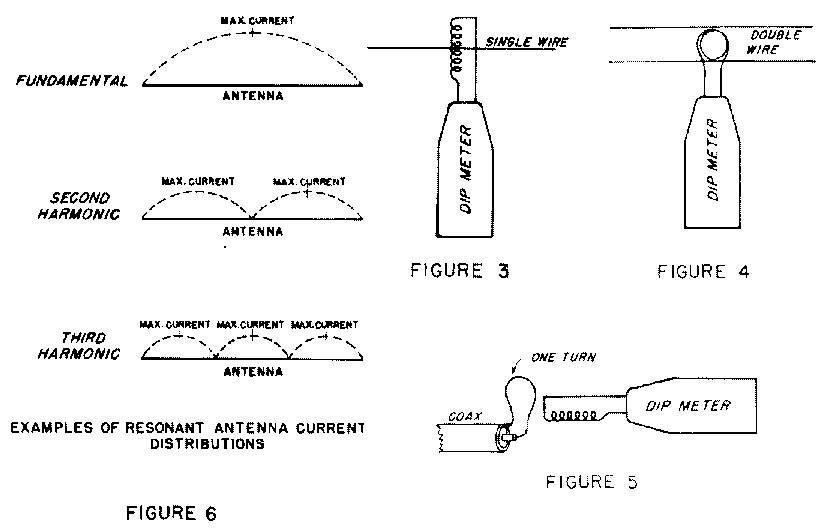
Generally, the resonant frequency of an antenna is measured by coupling the coil of the instrument to the part of the antenna with a current maximum. Although points of voltage maximum may be used, they are best avoided due to the increased possibility of spurious dips. See fig3-6.

The adjustment of the instrument is then the same as for LC circuits. For example, the halfwave antenna has a current maximum at the centre. The driven element in a beam antenna is usually a halfwave. When its frequency is to be determined, it is nessesary to disconnect all feeders and short out all breaks so introduced.
An antenna may also be operated on any multiple of its fundamental frequency. When this operation is desired, it is clarifying to sketch the current variation along the length of the antennae and make the frequency determination at one of the points of current maximum. For this frequency determination it is also nessesary to disconnect all transmission lines and short out any breaks.
The resonant frequency of a transmission line may be measured by concidering it as similar to the folded section of an antenna. The instrument is coupled to a shorted end of the transmission line and measurement is made as for an LC circuit. A sketch of the probable current distribution is helpful in determining the harmonic mode of operation. See fig7

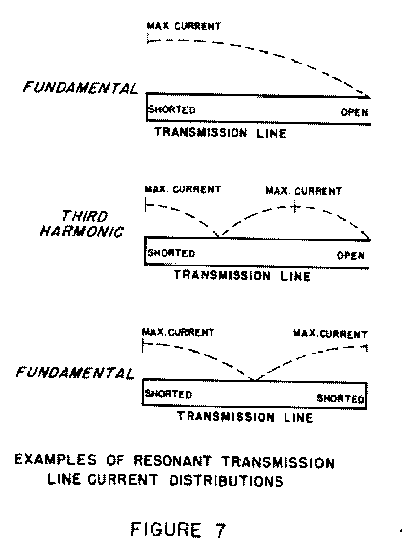
. For instance a quarterwave transmission line with the far end open is similar to a halfwave antennae and resonances will be found approximately at odd multiples of the fundamental frequency. When a transmission line is shorted at the far end, it may be concidered as two quarterwave transmission lines placed back to back. The resonant frequency is then approximately twice that found with the far end open.
When the transmission line is terminated in a pure resistance equal to its characteristic impedance, it will be found that the resonances will disappear. Any other load will cause resonances to reappear except at those frequencies at which the load on the transmission line is equal to its characteristic impedance. These facts can be used to load a transmission line to a high degree of accuracy.

Signal Generator
================
The instrument can be used as a source of signal in primary alignment of recievers. The amount of pickup by the reciever is varied by adjusting the position or distance of the instrument. The output signal is unmodulated, so that an R.F type of signal tracer is nessesary for indication the proper alignment of the tuned circuits. The "S" meter, in some recievers, may be used as an indicating device for alignment as long as the signal is kept at a low value to prevent AGC action, or the AGC may be disabled during alignment. If the instrument has a modulating facility then an audio type signal tracer may be used for alignment.
The instrument is a conveniant, if unstable, source of marker signals when using a sweep generator or Wobbulator. In this case also, the intensity of the marker may be varied by adjusting the position or distance of the instrument from the circuit under test.
For isolation, markers and test signals may be fed to various circuits by means of a transmission line. The input of the transmission line should be shorted with a loop , Fig5, that is lightly coupled to the coil in the instrument. The output of the transmission line is then fed into the equipment under test by any convenient means.

Signal Intensity Meter and Monitor
==================================
( Diode switch ON, if fitted. )
In this case, the instrument functions as an R.F. Pickup device or an Absorbtion Wavemeter where the meter deflection is proportional to the signal being picked up by the coil. The sensitivity may be increased by coupling the coil of the instrument to an antenna or transmission line extension, Fig5. As a signal intensity or field strength meter, the instrument is useful in:

1. Relative Field strength measurements
2. Neutralisation of amplifiers
3. Harmonic and parasitic analysis
4. Investigating standing waves on open line feeders

Inserting a phone jack into the "phone socket" usually disconnects the meter and enables modulation on the incoming signal to be heard. The instrument may then be used for determination of:

1. Hum and noise
2. Distortion
3. Audio quality

When used in this mode extreme care is needed to prevent electrocution when working on high energy circuits

Special Uses 1a,1b - Measuring Mutual Inductance and Coupling Coefficient
=========================================================================
Connect the two coils in series and the combination across a standard capacitor. Measure the resonant frequency and determine the the combined inductance as outlined in an earlier paragraph under "Applications - LC circuits". The connections to one of the coils is then reversed and the inductance of the combination is again determined. The effective mutual inductance M between the the two coils is equal to one fourth the difference between the two resultant measurements.
Having determined M from the above paragraph. Measure the inductance of each coil leaving the other coil open circuit. The coefficient of coupling K is given by the following formula:

K= M/ square root of(L1*L2)

where M is the mutual inductance and L1, L2 are the self inductances of the two coils respectivly.

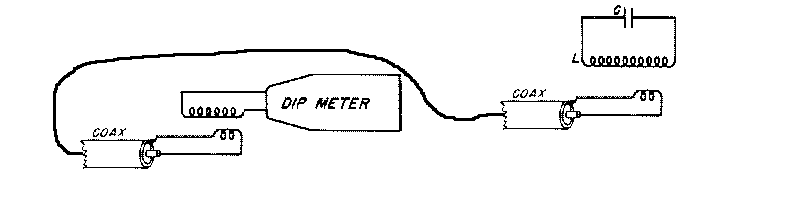
Special uses 2 - Measurement of Coax length
===========================================
Open circuit one end of the cable and short the other end with a short loop and couple the instrument to this loop, see Fig5, then starting at the lowest frequency, note the frequency of the successive dips. The fundamental resonanant frequency ( based on a quarterwave ) is approximately equal to one half the difference between two successive dips.
The physical length of the cable may now be calculated by the following formula:

L =(246*k)/f

where L is the length in feet, f is the resonant frequency in Mhz and k is the velocity factor of the cable ( usually 0.66 for solid dielectric ). It follows that the Velocity factor k can also be determined if the length of the cable is known.

Special uses 3 - crystal tester/marker
======================================
In many instruments the design is such that if a crystal is inserted in the coil socket it will oscillate at its fundamental frequency and an indication of oscillation will be given on the dip meter, crystal activity can be estimated by the amount of deflection. This signal is far more stable than useing a Coil and can be used as a Marker signal